(著)山たー
急に必要になったのでメモとして残しておく。1次元混合ガウス回帰という名前が正しいか分からないが、解きたい問題は次のようなデータに対して二乗誤差を最小化する混合ガウスモデルのパラメータを求めること。
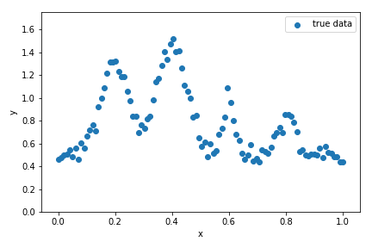
このデータに対し、次のようなモデルをfittingする。
$$ \hat{y} = \left[\sum_{i=1}^n g_i(x | a_i, \mu_i, \sigma_i)\right] + a_0 $$ ただし、 $g_i(x | a_i, \mu_i, \sigma_i) := a_i\exp\left[-\frac{(x-\mu_i)^2}{2\sigma_i^2}\right]$とする。
ガウス分布の数を固定した場合
実装
何個のガウス分布で推定できるか分かっている場合。まずテストデータを生成。山は4つにしておく。
import numpy as np
from scipy.optimize import leastsq
import matplotlib.pyplot as plt
from tqdm import tqdm
import math
"""Setting up test data"""
def gaussian_func(x, A, mu, sigma):
return A * np.exp( - (x - mu)**2 / (2 * sigma**2))
num_peak = 4
A = np.array([0.8, 1, 0.5, 0.3]) #np.random.rand(num_peak)
mu = np.array([0.2, 0.4, 0.6, 0.8])
sigma = np.array([0.05, 0.05, 0.02, 0.03])
num_sample = 100
x = np.linspace(0, 1, num_sample)
y_true = np.random.normal(0.5, 0.05, len(x))
for i in range(num_peak):
y_true += gaussian_func(x, A[i], mu[i], sigma[i])
次にscipy.optimize.leastsqを用いて、二乗誤差を最小化するパラメータを求める。このとき、初期値をランダムに選びなおして最小化を行う。最終的に二乗誤差を最小化するパラメータを最適なパラメータとする。
"""Solving"""
def residual(p, y, x):
y_fit = p[0]
for i in range(num_peak):
y_fit += gaussian_func(x, p[3*i+1], p[3*i+2], p[3*(i+1)])
error = y - y_fit
return error
max_iter = 100
sse = 1e5 # set initial loss large
num_param = num_peak*3 + 1
for i in tqdm(range(max_iter)):
p = np.random.rand(num_param) # initial guesses for leastsq
plsq, ier = leastsq(residual, p, args = (y_true, x))
sse_i = np.sum(residual(plsq, y_true, x)**2)
if sse_i < sse:
sse = sse_i
plsq_opt = plsq
最後に結果をプロットする。後のためにBICも求めておく。
"""plot results"""
y_estimated = plsq_opt[0]
for i in range(num_peak):
y_estimated += gaussian_func(x, plsq_opt[3*i+1], plsq_opt[3*i+2],
plsq_opt[3*(i+1)])
# BIC = n* ln(sse/n) + k*ln(n)
bic = num_sample*math.log(sse/num_sample) + num_param*math.log(num_sample)
print("BIC:", bic)
fig, ax = plt.subplots(figsize=(6, 4))
plt.scatter(x, y_true, label='true data')
plt.plot(x, y_estimated, label="estimated curve", color="r")
ax.set_ylim(0, 2)
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.legend()
plt.tight_layout()
plt.savefig("mix_gauss_fit.png")
plt.show()
plt.close()
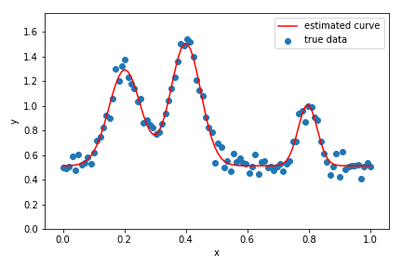
結果

最適なガウス分布の数をBICにより求める
何個のガウス分布でfittingすればいいか分からない場合。BICを計算して最小化するものを選び出す。
実装
import numpy as np
from scipy.optimize import leastsq
import matplotlib.pyplot as plt
from tqdm import tqdm
import math
"""Setting up test data"""
def gaussian_func(x, A, mu, sigma):
return A * np.exp( - (x - mu)**2 / (2 * sigma**2))
num_peak_true = 3
A = np.array([0.8, 1, 0.5]) #np.random.rand(num_peak)
mu = np.array([0.2, 0.4, 0.8])
sigma = np.array([0.05, 0.05, 0.03])
num_sample = 100
x = np.linspace(0, 1, num_sample)
y_true = np.random.normal(0.5, 0.05, len(x))
for i in range(num_peak_true):
y_true += gaussian_func(x, A[i], mu[i], sigma[i])
"""Solving"""
max_num_peak = 6
max_iter = 100
bic = 1e5
bic_arr = np.zeros(max_num_peak)
for num_peak in range(1, max_num_peak+1):
def residual(p, y, x):
y_fit = p[0]
for i in range(num_peak):
y_fit += gaussian_func(x, p[3*i+1], p[3*i+2], p[3*(i+1)])
error = y - y_fit
return error
sse = 1e5 # set initial loss large
num_param = num_peak*3 + 1
for i in tqdm(range(max_iter)):
p = np.random.rand(num_param) # initial guesses for leastsq
plsq, ier = leastsq(residual, p, args = (y_true, x))
sse_i = np.sum(residual(plsq, y_true, x)**2)
if sse_i < sse:
sse = sse_i
plsq_opt = plsq
# BIC = n* ln(sse/n) + k*ln(n)
bic_i = num_sample*math.log(sse/num_sample) + num_param*math.log(num_sample)
print("num of peak: ", num_peak, "BIC:", bic_i)
bic_arr[num_peak-1] = bic_i
if bic_i < bic:
bic = bic_i
num_peak_estimated = num_peak
plsq_global_opt = plsq_opt
"""plot results"""
y_estimated = plsq_global_opt[0]
for i in range(num_peak_estimated):
y_estimated += gaussian_func(x, plsq_global_opt[3*i+1], plsq_global_opt[3*i+2],
plsq_global_opt[3*(i+1)])
# gaussian fit
fig, ax = plt.subplots(figsize=(6, 4))
plt.scatter(x, y_true, label='true data')
plt.plot(x, y_estimated, label="estimated curve", color="r")
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_ylim(0, 1.75)
plt.legend()
plt.tight_layout()
plt.savefig("mix_gauss_fit.png")
plt.show()
plt.close()
# BIC
x_bic = np.arange(1,max_num_peak+1, 1)
fig, ax = plt.subplots(figsize=(6, 4))
plt.plot(x_bic, bic_arr, color="r")
ax.set_xlabel('Number of Gaussian fit')
ax.set_ylabel('BIC')
plt.xticks(x_bic)
plt.tight_layout()
plt.savefig("bic.png")
plt.show()
plt.close()
結果
ガウス分布の数に対するBICの変化。ちゃんと設定通りの3のときに最小になっている。

コメントをお書きください
neiljiohu (火曜日, 16 7月 2024 14:46)
无论您的学科、主题或最后期限是什么,我们都愿意帮助您完成Essay。我们98%以上的客户保持满意,因为我们从不吝惜我们的服务质量。我们的Essay代写 https://www.essayghostwriting.com/ 平台是您仅有的正确选择! 我们的专家团队知道如何完成所有学术领域和学术水平的作业。