(著)山たー・優曇華院
Hamiltonian Descent Method (arxiv)の「実装の」解説です。Githubの実装はこれです。
先に言っておきますが、現時点でニューラルネットワークの学習に有効に使えるものではありません(optimizerを実装して検証しましたが、ちゃんと学習が進みませんでした。実装があってるのかは微妙ですが)。しかも、自分はちゃんとこの論文の意義を理解してない感があります。
(追記)ちゃんと実装したら最適化できるようです。自分はcifar10でやってたから駄目だったのかも。
→ Hamiltonian Descent Methods を chainer で実装した
数学的な詳しい解説は
→ Hamiltonian Descent Methods ~より広範なクラスで1次収束を達成する最適化手法~
この記事はとりあえず実装しましたという内容です。かしこみ。
Hamiltonian Descentについて
論文の冒頭にある図です。
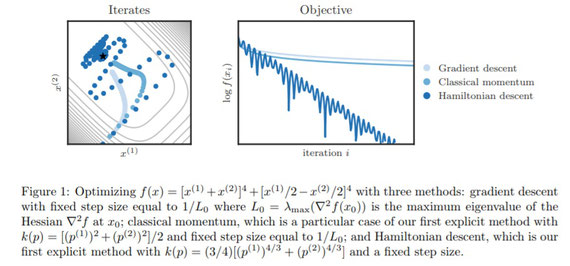
今回は、このHamiltonian Descent法の『実装』の解説をしてみます。『実装』の解説なのは、数式による議論が半分以上分からないためです。ぜひとも数学科の人の解説が読みたいものです。
Hamiltonian Descentの数式
First Explicit Methodについて
論文中では1つの陰解法(implicit method)と2つの陽解法(explicit method)が紹介されています。陰解法と陽解法についてはWikipediaに書いていますが、ざっくり説明すると、陰解法ではタイムステップごとに方程式を解く必要があるのに対し、陽解法では漸化式を使って順番に出せるということです。なので、陽解法の方が大きく近似が必要なものの、計算量が少なくて済みます。自分の実装は陽解法の1つ、First explicit methodです。
Chainerを用いた実装
さて、いよいよ実装の話です。式を見ると分かりますが、2回gradientを計算する必要があります。1回だけの計算で済ませる方法もありますが、後で説明します。
Pythonを使って数値微分・自動微分するにはsympyやautogradなど、またDeep LearningのためのライブラリであるChainerやPytorchを用いるのが良いでしょう。今回はChainerを用いた実装を紹介します。
計算の実装
まず、必要なライブラリをインポートします。
import numpy as np import chainer.functions as F from chainer import Variable import matplotlib.pyplot as plt from matplotlib.colors import LogNorm
# Define functions
def f(x): # Potential energy function
return (x[0] + x[1])**4 + (x[0]/2 - x[1]/2)**4
def k(p, exponent=4/3): # Kinetic energy function
return F.sum(F.absolute(p)**exponent)/exponent
このkはハイパーパラメータならぬハイパーファンクションで、関数をうまく選ぶ必要があります。
次にxとpの初期値、およびハイパーパラメータを定義します。
# Initialization i = 0 x_i = np.array([2., 1.]) p_i = np.array([0., 0.]) # Hyper parameters gamma = 0.2 epsilon = 0.01 delta = 1/(1 + gamma*epsilon)
解が収束するまでwhileループを回します。
while(1): # Untill x converged
""" First Explicit Method """
# Compute grad f
x_ivar = Variable(x_i)
potential_energy = f(x_ivar)
potential_energy.backward()
grad_f = x_ivar.grad
# Equation 1
p_ip1 = delta*p_i - epsilon*delta*grad_f
# Compute grad k
p_ip1var = Variable(p_ip1)
exponent = 4/3
kinetic_energy = k(p_ip1var, exponent)
kinetic_energy.backward()
grad_k = p_ip1var.grad
# Equation 2
x_ip1 = x_i + epsilon*grad_k
# Update i
i += 1
# Check convergence
if np.all(abs(x_i - x_ip1) < 1e-6):
break
# Update x and p
p_i = p_ip1
x_i = x_ip1
結果
冒頭の図が再現できました。
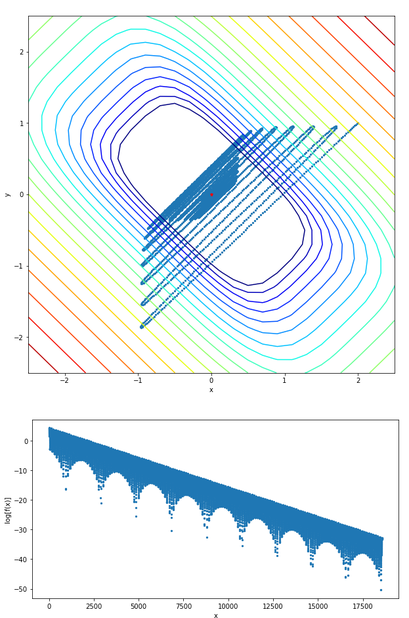
まとめ
・Hamiltonian Descent法を用いると凸関数最適化が高精度で行える。
・非凸関数の場合、パラメータ調節がうまくないと最適化できない場合がある。
・ニューラルネットワークの最適化に応用するには運動エネルギー関数の研究が必要。
参考にしたサイト
結果の描画のためのコードを参考にしました
・Visualizing and Animating Optimization Algorithms with Matplotlib | Louis Tiao
コメントをお書きください