Python · 2018/07/16

PythonでGaussian Fitting

（著）山たー・優曇華院

ScipyでGaussian Fittingして標準誤差を出すだけ。Scipyで非線形最小二乗法によるフィッティングをする。最適化手法はLevenberg-Marquardt法を使う。

結果

       Estimate  Std. Error      lwCI      upCI
mu    -0.043331    0.098086 -0.235575  0.148914
sigma  1.133417    0.080087  0.976451  1.290384

コード

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
from scipy.stats import norm

# gaussian function
def gaussian_func(x, mu, sigma):
    return 1/(sigma * np.sqrt(2 * np.pi)) * np.exp( - (x - mu)**2 / (2 * sigma**2))

# generate toy data
x = np.arange(-5,5, 0.5)
y = gaussian_func(x, 0, 1) + np.random.normal(0, 0.05, len(x))
plt.scatter(x,y)

# estimate optimal parameter & parameter covariance
popt, pcov = curve_fit(gaussian_func, x, y)

# plot result
xd = np.arange(x.min(), x.max(), 0.01)
estimated_curve = gaussian_func(xd, popt[0],popt[1])
plt.plot(xd, estimated_curve, label="Estimated curve",color="r")
plt.legend()
plt.savefig("gaussian_fitting.png")
plt.show()

# estimate standard Error
StdE = np.sqrt(np.diag(pcov))

# estimate 95% confidence interval
alpha=0.025
lwCI = popt + norm.ppf(q=alpha)*StdE
upCI = popt + norm.ppf(q=1-alpha)*StdE

# print result
mat = np.vstack((popt,StdE, lwCI, upCI)).T 
df=pd.DataFrame(mat,index=("mu", "sigma"),
                columns=("Estimate", "Std. Error", "lwCI","upCI"))
print(df)

共分散行列はJacobianを$J$として、 $$ \text{Cov}=(J^TJ)^{-1} $$ で求めている。対角成分の平方根を取って標準誤差となる。

ピーク値も推定する場合

優曇華院が修正したもの。Gaussianのピーク値Aも変数として推定したい場合は次のようにする。

コード

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
from scipy.stats import norm

# gaussian function
def gaussian_func(x, A, mu, sigma):
    return A * np.exp( - (x - mu)**2 / (2 * sigma**2))

# generate toy data
x = np.array([2.45, 2.55, 2.65, 2.75, 2.85, 2.95, 3.05, 3.15, 3.25, 3.35])
y = np.array([0.000333333333401242, 22.0373333333334, 142.074333333333, 383.444666666667, 602.815, 611.185333333333, 417.555666666667, 154.926, 13.2963333333335, 0])
plt.scatter(x,y)

# initial_guess_of_parameters
# この値はソルバーとかで求めましょう．
parameter_initial = np.array([652, 2.9, 1.3])

# estimate optimal parameter & parameter covariance
popt, pcov = curve_fit(gaussian_func, x, y, p0=parameter_initial)

# plot result
xd = np.arange(x.min(), x.max(), 0.01)
estimated_curve = gaussian_func(xd, popt[0], popt[1], popt[2])
plt.plot(xd, estimated_curve, label="Estimated curve", color="r")
plt.legend()
plt.savefig("gaussian_fitting.png")
plt.show()

# estimate standard Error
StdE = np.sqrt(np.diag(pcov))

# estimate 95% confidence interval
alpha=0.025
lwCI = popt + norm.ppf(q=alpha)*StdE
upCI = popt + norm.ppf(q=1-alpha)*StdE

# print result
mat = np.vstack((popt,StdE, lwCI, upCI)).T
df=pd.DataFrame(mat,index=("A", "mu", "sigma"),
columns=("Estimate", "Std. Error", "lwCI", "upCI"))
print(df)

結果

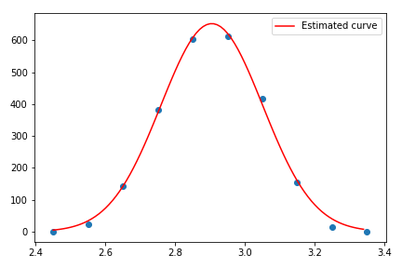
         Estimate  Std. Error        lwCI        upCI
A      652.173659   11.491564  629.650608  674.696710
mu       2.904722    0.002973    2.898895    2.910548
sigma   -0.146120    0.002973   -0.151948   -0.140293