Hodgkin Huxley.py
Hodgkin-HuxleyモデルのPythonでの実装として、Hodgkin Huxley.pyというものがありました。実行すると次のようになります。
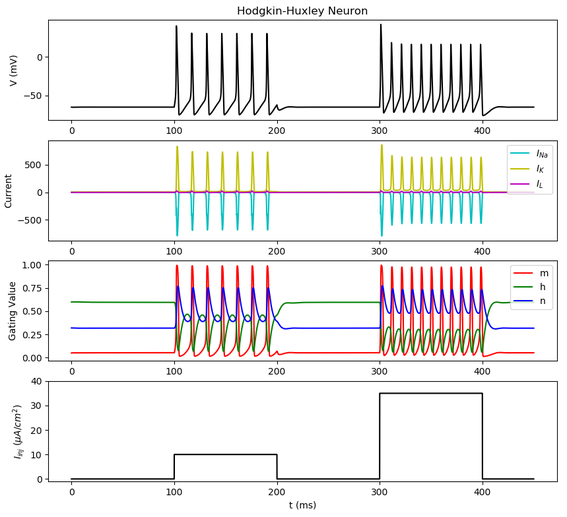
1番目が膜電位、2番目が膜電流、3番目がイオンチャネルの活性化・不活性化パラメータ、4番目が刺激電流の時間変化を表しています。
この図について見るべきところは、刺激電流が強くなっても、活動電位の形状は変化せず、発火頻度が高くなるという点です。
今回は、この実装に手を加えて時間変化をアニメーションで見れるようにしてみました。
Hodgkin-Huxleyの方程式
アニメーションに移る前に、Hodgkin-Huxleyの方程式とその実装を見ておきましょう。Hodgkin-Huxleyの方程式は4つの微分方程式と6つの関係式からなります。
6つの変数と7つの定数
変数は
$I_m$:全膜電流(刺激電流) $[\mu \text{A/cm}^2]$
$V$ :膜電位 $[\text{mV}]$
$t$ :時間 $[\text{msec}]$
$m$ :Naコンダクタンスの活性化パラメータ
$h$ :Naコンダクタンスの不活性化パラメータ
$n$ :Kコンダクタンスの活性化パラメータ
の6つです。
$I_m$:全膜電流(刺激電流) $[\mu \text{A/cm}^2]$
$V$ :膜電位 $[\text{mV}]$
$t$ :時間 $[\text{msec}]$
$m$ :Naコンダクタンスの活性化パラメータ
$h$ :Naコンダクタンスの不活性化パラメータ
$n$ :Kコンダクタンスの活性化パラメータ
の6つです。
定数は7つあり、静止膜電位が$-65\text{mV}$の場合、 \begin{align*} C_m=1.0, g_{Na}=120, g_K=36, g_l=0.3\\ E_{Na}=50.0, E_K=-77, E_l=-54.387 \end{align*} です。
微分方程式
微分方程式は次の4つ。
\begin{align*} I_m&=C_{m}\frac {dV}{dt}+{\bar {g}}_{K}n^{4}(V-E_{K})+{\bar {g}}_{Na}m^{3}h(V-E_{Na})+{\bar {g}}_{l}(V-E_{l})\\ (\iff \frac {dV}{dt}&=\left[I_m-{\bar
{g}}_{K}n^{4}(V-E_{K})+{\bar {g}}_{Na}m^{3}h(V-E_{Na})+{\bar {g}}_{l}(V-E_{l})\right]/C_m)\\ \frac{dn}{dt}&=\alpha _{n}(V)(1-n)-\beta_{n}(V)n\\ \frac{dm}{dt}&=\alpha
_{m}(V)(1-m)-\beta_{m}(V)m\\ \frac{dh}{dt}&=\alpha _{h}(V)(1-h)-\beta_{h}(V)h \end{align*}
実装は次のようになります。
def I_Na(V, m, h):
"""Membrane current (in uA/cm^2): Sodium (Na = element name)"""
return g_Na * m**3 * h * (V - E_Na)
def I_K(V, n):
"""Membrane current (in uA/cm^2): Potassium (K = element name)"""
return g_K * n**4 * (V - E_K)
# Leak
def I_L(V):
"""Membrane current (in uA/cm^2): Leak"""
return g_L * (V - E_L)
def dALLdt(X, t):
global timecount
"""Integrate"""
V, m, h, n = X
dVdt = (I_inj(t, timecount) - I_Na(V, m, h) - I_K(V, n) - I_L(V)) / C_m
dmdt = alpha_m(V)*(1.0-m) - beta_m(V)*m
dhdt = alpha_h(V)*(1.0-h) - beta_h(V)*h
dndt = alpha_n(V)*(1.0-n) - beta_n(V)*n
return dVdt, dmdt, dhdt, dndt
関係式
微分方程式内の関数は以下の6つ。
\begin{align*} \alpha_{m}(V)&={\frac {0.1(25-V)}{\exp {\big (}{\frac {25-V}{10}}{\big )}-1}}\\ \beta_{m}(V)&=4\exp {(-V/18)}\\ \alpha_{h}(V)&=0.07\exp {(-V/20)}\\ \beta_{h}(V)&={\frac
{1}{\exp {\big (}{\frac {30-V}{10}}{\big )}+1}}\\ \alpha_{n}(V)&={\frac {0.01(10-V)}{\exp {\big (}{\frac {10-V}{10}}{\big )}-1}}\\ \beta_{n}(V)&=0.125\exp {(-V/80)} \end{align*}
実装は次のようになります。静止膜電位$V$は任意の値を取れるので、$V=-65\text{mV}$となるように上の式の $-V$ を $-(V+65)$ に置き換えています。
実装は次のようになります。静止膜電位$V$は任意の値を取れるので、$V=-65\text{mV}$となるように上の式の $-V$ を $-(V+65)$ に置き換えています。
def alpha_m(V):
"""Channel gating kinetics. Functions of membrane voltage"""
return 0.1*(V+40.0)/(1.0 - np.exp(-(V+40.0) / 10.0))
def beta_m(V):
"""Channel gating kinetics. Functions of membrane voltage"""
return 4.0*np.exp(-(V+65.0) / 18.0)
def alpha_h(V):
"""Channel gating kinetics. Functions of membrane voltage"""
return 0.07*np.exp(-(V+65.0) / 20.0)
def beta_h(V):
"""Channel gating kinetics. Functions of membrane voltage"""
return 1.0/(1.0 + np.exp(-(V+35.0) / 10.0))
def alpha_n(V):
"""Channel gating kinetics. Functions of membrane voltage"""
return 0.01*(V+55.0)/(1.0 - np.exp(-(V+55.0) / 10.0))
def beta_n(V):
"""Channel gating kinetics. Functions of membrane voltage"""
return 0.125*np.exp(-(V+65) / 80.0)
実装1
コード
元のコードはclassを用いて記述されていましたが、扱いづらかったので（というとプログラミング力が低いなあと思いますが）、classを取っ払いました。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import scipy.integrate as integrate
#const.
C_m = 1.0 #membrane capacitance, in uF/cm^2
g_Na = 120.0 #Sodium (Na) maximum conductances, in mS/cm^2
g_K = 36.0 #Postassium (K) maximum conductances, in mS/cm^2
g_L = 0.3 #Leak maximum conductances, in mS/cm^2
E_Na = 50.0 #Sodium (Na) Nernst reversal potentials, in mV
E_K = -77.0 #Postassium (K) Nernst reversal potentials, in mV
E_L = -54.387 #Leak Nernst reversal potentials, in mV"""
dt = 0.01
t = np.arange(0.0, 50.0, dt) #The time to integrate over
len_t = len(t)
timestep = 20 #timestep
timecount = 0 #global
def alpha_m(V):
"""Channel gating kinetics. Functions of membrane voltage"""
return 0.1*(V+40.0)/(1.0 - np.exp(-(V+40.0) / 10.0))
def beta_m(V):
"""Channel gating kinetics. Functions of membrane voltage"""
return 4.0*np.exp(-(V+65.0) / 18.0)
def alpha_h(V):
"""Channel gating kinetics. Functions of membrane voltage"""
return 0.07*np.exp(-(V+65.0) / 20.0)
def beta_h(V):
"""Channel gating kinetics. Functions of membrane voltage"""
return 1.0/(1.0 + np.exp(-(V+35.0) / 10.0))
def alpha_n(V):
"""Channel gating kinetics. Functions of membrane voltage"""
return 0.01*(V+55.0)/(1.0 - np.exp(-(V+55.0) / 10.0))
def beta_n(V):
"""Channel gating kinetics. Functions of membrane voltage"""
return 0.125*np.exp(-(V+65) / 80.0)
def I_Na(V, m, h):
"""Membrane current (in uA/cm^2): Sodium (Na = element name)"""
return g_Na * m**3 * h * (V - E_Na)
def I_K(V, n):
"""Membrane current (in uA/cm^2): Potassium (K = element name)"""
return g_K * n**4 * (V - E_K)
# Leak
def I_L(V):
"""Membrane current (in uA/cm^2): Leak"""
return g_L * (V - E_L)
def I_inj(t,timecount):
y = np.sin((t + timecount*dt*timestep)/5)
I = 30*np.where(y>0,1,0)
return I
def dALLdt(X, t):
global timecount
"""Integrate"""
V, m, h, n = X
dVdt = (I_inj(t, timecount) - I_Na(V, m, h) - I_K(V, n) - I_L(V)) / C_m
dmdt = alpha_m(V)*(1.0-m) - beta_m(V)*m
dhdt = alpha_h(V)*(1.0-h) - beta_h(V)*h
dndt = alpha_n(V)*(1.0-n) - beta_n(V)*n
return dVdt, dmdt, dhdt, dndt
fig, (ax1, ax2, ax3,ax4) = plt.subplots(nrows=4,ncols=1, figsize=(7,10))
#fig.tight_layout()
#animationの1step
def update(i):
global X, X0, timecount
#y0の初期値の設定
if i ==0:
X0 = [-65, 0.05, 0.6, 0.32]
#現在描写されているグラフを消去
ax1.cla()
ax2.cla()
ax3.cla()
ax4.cla()
timecount = i
#微分方程式を解く
X = integrate.odeint(dALLdt, X0, t)
V = X[:,0]
m = X[:,1]
h = X[:,2]
n = X[:,3]
ina = I_Na(V, m, h)
ik = I_K(V, n)
il = I_L(V)
#timestep後のyの値を次のステップでのy0の値に更新する
X0 = (V[timestep], m[timestep], h[timestep], n[timestep])
#描画
ax1.set_title('Hodgkin-Huxley Neuron')
ax1.plot(t, V, 'k')
ax1.plot(t[len_t-1],V[len_t-1],'ko')
ax1.set_ylabel('V (mV)')
ax1.set_ylim([-80,50])
ax2.grid()
ax2.plot(t, ina, 'c', label='$I_{Na}$')
ax2.plot(t, ik, 'y', label='$I_{K}$')
ax2.plot(t, il, 'm', label='$I_{L}$')
ax2.plot(t[len_t-1],ina[len_t-1],'co')
ax2.plot(t[len_t-1],ik[len_t-1],'yo')
ax2.plot(t[len_t-1],il[len_t-1],'mo')
ax2.set_ylabel('Current')
ax2.set_ylim([-900,900])
ax2.grid()
ax2.legend(bbox_to_anchor=(0, 1),
loc='upper left',
borderaxespad=0)
ax3.plot(t, m, 'r', label='m')
ax3.plot(t, h, 'g', label='h')
ax3.plot(t, n, 'b', label='n')
ax3.plot(t[len_t-1],m[len_t-1],'ro')
ax3.plot(t[len_t-1],h[len_t-1],'go')
ax3.plot(t[len_t-1],n[len_t-1],'bo')
ax3.set_ylabel('Gating Value')
ax3.legend(bbox_to_anchor=(0, 1),
loc='upper left',
borderaxespad=0)
i_inj_values = [I_inj(t,timecount) for t in t]
ax4.plot(t, i_inj_values, 'k')
ax4.plot(t[len_t-1], i_inj_values[len_t-1],'ko')
ax4.set_xlabel('t (ms)')
ax4.set_ylabel('$I_{inj}$ ($\\mu{A}/cm^2$)')
ax4.set_ylim(-2, 40)
ani = animation.FuncAnimation(fig, update, interval=100,
frames=100)
plt.show() #表示
#ani.save("Hodgkin-Huxley.mp4") #保存
結果
結果は次のようになりました。描画速度はFitzHugh-Nagumoモデルに比べると遅いです。計算量が多いので当然ですが。
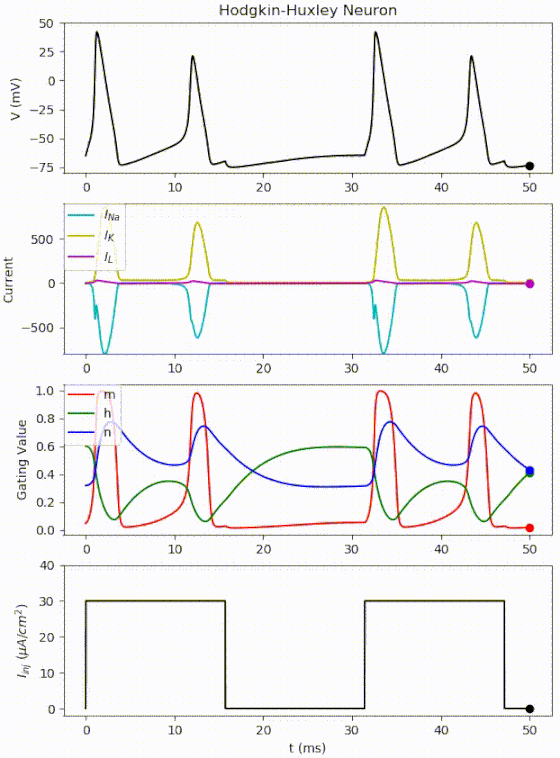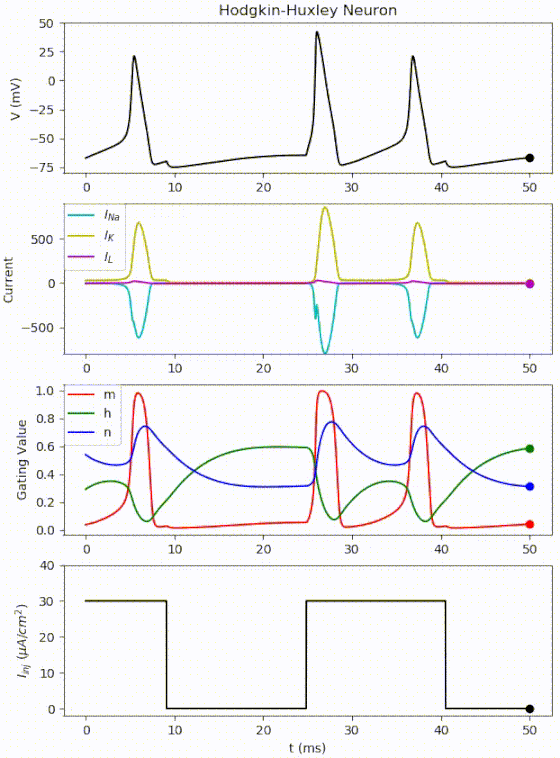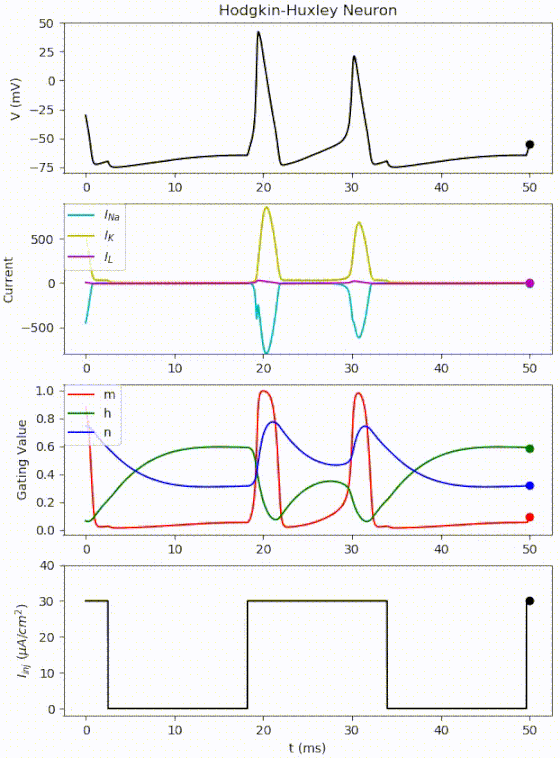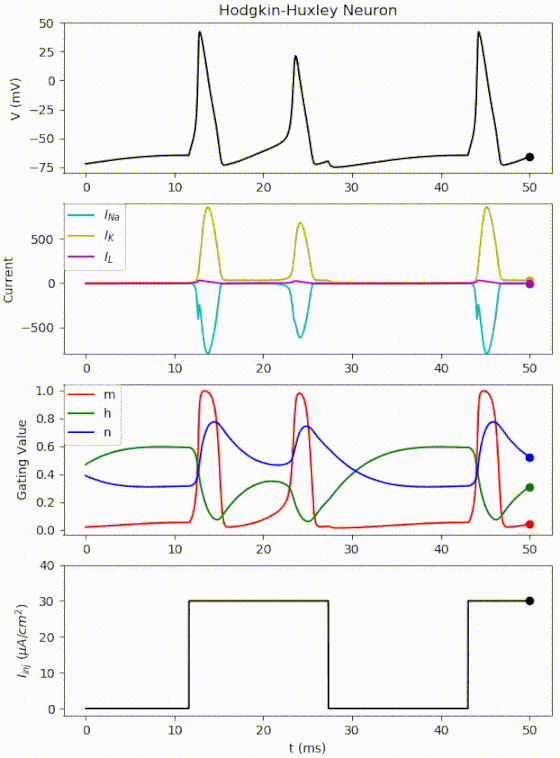
おさらいですが、mはNaコンダクタンスの活性化パラメータ、hはNaコンダクタンスの不活性化パラメータ、nはKコンダクタンスの活性化パラメータです。
よく見ると、
①刺激が閾値を超えるとNa+チャネルが開口し、細胞内にNa+が流入（脱分極）
②少し遅れてK+チャネルが開口し、細胞外にK+が流出（再分極）
という流れに従って各変数が時間変化していることが分かります。
実装2
矩形波の振幅を変動させてみました。
コード
刺激電流を定義する関数を次のように変更します。
def I_inj(t,timestep):
y1 = np.sin((t + timecount*dt*timestep)/5)
y2 = np.sin((t + timecount*dt*timestep)/10) #周期はy1の2倍
#sin波をstep関数に変換
sq_y1 = np.where(y1 > 0,1,0)
sq_y2 = np.where(y2 > 0,1,0)
I = 10*sq_y1*sq_y2 + 35*sq_y1*(1-sq_y2)
return I
結果
参考文献
・宮川 博義, 井上 雅司,『ニューロンの生物物理 第2版』,2013,丸善出版,p.50
コメントをお書きください