keras · 2018/05/13

KerasによるGraph Convolutional Networks

(著)山たー

Thomas Kipf氏(https://github.com/tkipf)による、KerasでのGraph Convolutional Networks(GCN)の実装を見てみます。論文は"Thomas N. Kipf, Max Welling, Semi-Supervised Classification with Graph Convolutional Networks (ICLR 2017)"(arxiv)です。

畳み込みとCNN

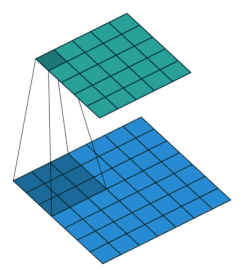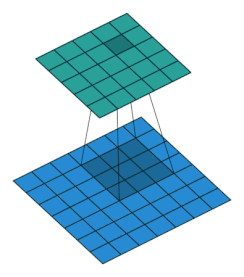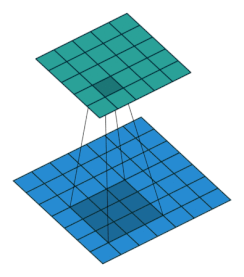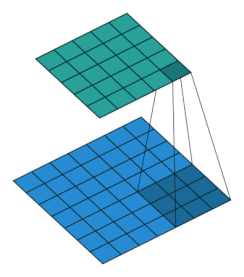
まずCNNにおける畳み込みからおさらい。入力テンソルをスライスしてフィルターと畳み込みをします。

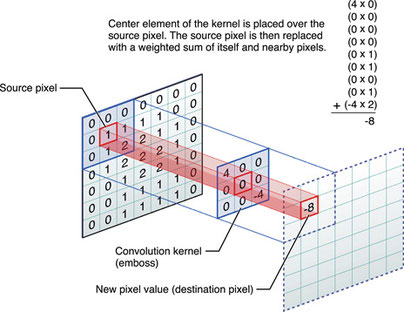
（画像の引用元）：Convolution Matrix Pictures to Pin on Pinterest - PinsDaddy

アニメーションで見ると次のgifのような感じ。フィルターをスライドさせながら、行列（テンソル）の要素とフィルターの要素の積を取り、足し合わせることで次層の入力としています。

（画像の引用元）：Convolution arithmetic

このようにCNNで畳み込めるデータはユークリッド空間上のものです。これがどういう意味かについては次の図を見てください。

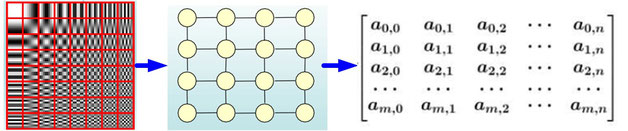
（画像の引用元）：如何理解 Graph Convolutional Network（GCN）？ - 知乎

ユークリッド空間上のデータは行列やテンソルとして表現できます。言い換えれば近傍の情報を行列やテンソル内の近傍の要素として格納することができるということです。しかし、データの中にはユークリッド構造でないものもあります。

グラフとネットワーク構造（非ユークリッド構造）

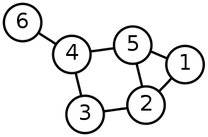
ユークリッド構造でないデータ構造として、グラフ(graph)があります(Wikipedia)。円グラフとか棒グラフのグラフではなく、グラフ理論のグラフです。この意味のグラフは頂点(node)と辺(edge)からなるネットワーク構造です。以下は6つの頂点と7つの辺があるグラフです。

グラフの適用例は広く、生体内での複雑な化合物の作用もグラフですし、神経回路もグラフ構造、はたまた、人間関係、商品のやり取りなど、何かしらの繋がりは全てグラフで記述できます。実は有機化合物もグラフだったりします。

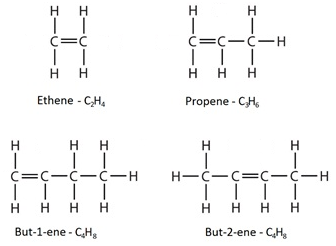
原子が頂点、結合が辺というわけです。

余談ですが、グラフの本だと『グラフ理論の魅惑の世界(amazon)』というのが面白かったです。

有名なグラフ構造のデータセットとして、下図のような「空手クラブのネットワーク」(Brandes et al., 2008)があります。

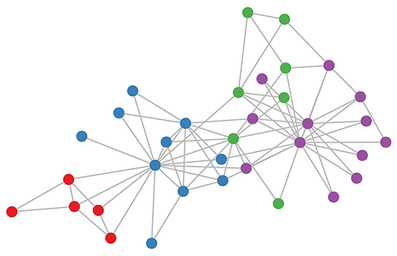
（画像の引用元）：Graph Convolutional Networks : Thomas Kipf

このようなグラフの情報は非ユークリッド空間上でのみ表せます。

Graph Convolutional Networks

さて、本題のGraph Convolutionです。普通のConvolutional Neural Networks(CNN)は「画像を入力として、畳み込み演算を適用する」ニューラルネットワークです。なので対比させて考えればGCNNは「グラフに対して畳み込み演算を実行する」ということになります。

それで、「グラフに畳み込み演算ってどないすんねん」という話ですが、Graph Fourier変換というものを行います。

間違っている可能性大ですが

グラフに畳み込み演算適用できなくね。無理くね。

→適用できるようなデータ空間に写像すればよくね。

（グラフ信号にフーリエ変換を適用してグラフスペクトル領域に変換する）

→畳み込みした後、元のデータ空間に逆写像すればよくね。

→この一連の流れを「Graph Convolution」って呼ぼうぜ。

ということらしいです。

GCNの応用

・ネットワーク解析全般

・化合物の物性予測

・mRNA

(例)乳がんのサブタイプの推定：Hybrid Approach of Relation Network and Localized Graph Convolutional Filtering for Breast Cancer Subtype Classification

まず、出力は乳がんのサブタイプです（参照）。入力は次の2つを組み合わせたグラフです。まず、グラフの構造としてタンパク質とタンパク質の相互作用のネットワークを用意します。この状態では頂点に重みは付いていません。次にグラフ内のタンパク質に対応する遺伝子の遺伝子発現量を頂点の重みとします。こうしてできた重み付きグラフを入力として、GCNNとRN(related network)を組み合わせたモデルを用いて学習すると、高い精度(84%ぐらい)で乳がんのサブタイプが予測できたということです。

・自然言語処理

Thomas Kipf氏によるKerasでの実装

いよいよhttps://github.com/tkipf/keras-gcnの中身を見てみます。まずは、どのような課題を解くのかから見てみます。その後にGCNの実装の解説をします。

Coraデータセット

Keras-GCNのデフォルトのデータセットはCoraデータセットというものです。やりたいことは論文内の単語と引用・被引用によるネットワークから論文のクラスを推定することです。

Coraデータセットは機械学習の論文で構成されていて、それぞれの論文は、次の7つのクラスのいずれかに分類されます。

Case_Based

Genetic_Algorithms

Neural_Networks

Probabilistic_Methods

Reinforcement_Learning

Rule_Learning

Theory

これらの論文は、少なくとも1つの他の論文に引用されている、かつ引用している論文です。コーパスには全部で2708の論文があります。

論文の中の特徴的な単語の選び方は次の通りです。まず、ストップワード(stop word, 助詞など不要な語)を削除した後、さらに文書中に10未満しか出ないすべての単語を削除し、1433の特徴的な単語が選ばれています。

Coraデータセットは頂点2708, 辺5429, 各頂点の特徴量1433から成ります。それぞれの頂点が論文に対応し、頂点には特徴として1433の単語が重み付けられています（0か1）。辺は引用リンクによる繋がりを表しています。

元データはhttps://linqs.soe.ucsc.edu/dataにある

.content

.cites

の2つのファイル

1.cites

引用されている論文のID、引用している論文のID

5430のエッジ

2.content

<paper_id> <word_attributes>+ <class_label>

2708x1435の行列

論文ID+単語(1433)+class

(例)31336, 0,0,1,…,0,Neural_Networks

このデータを表すのにデータは2種類

ノード数をn, ノードにおける重みの数をとして

A = 隣接行列(Adjacency matrix)…n次正方行列

X = 特徴行列(ノードと重みの行列)…n×m行列

Coraデータセットでは隣接行列(A)が2708次正方行列で、そのうち1の要素（＝辺が存在する）の数は5430であり、特徴行列(X)が2708×1433の行列です。

Graph Convolutionの実装

1層の計算は次のようになっています。 $$ f(H^{(l)}, A) = \sigma\left( \hat{D}^{-\frac{1}{2}}\hat{A}\hat{D}^{-\frac{1}{2}}H^{(l)}W^{(l)}\right) $$ このうち、$\hat{D}^{-\frac{1}{2}}\hat{A}\hat{D}^{-\frac{1}{2}}$の部分はグラフ構造を表す一定の行列であるため、学習前に計算してしまいます。この計算はtrain.pyにあり、

if FILTER == 'localpool':
    """ Local pooling filters (see 'renormalization trick' in Kipf & Welling, arXiv 2016) """
    print('Using local pooling filters...')
    A_ = preprocess_adj(A, SYM_NORM)
    support = 1
    graph = [X, A_]
    G = [Input(shape=(None, None), batch_shape=(None, None), sparse=True)]

となっています。graph = [X, A_]が成形した入力となります。 Gはmodelの入力テンソルです。 sparse=Trueとなっていますが、これは生成するplaceholderをスパースにするための引数です。A_はscipy.sparseにより、sparseな行列で定義されています。もし、sparseでないとMemoryErrorが発生します。 preprocess_adjはutils.pyにある関数で、中身は

def normalize_adj(adj, symmetric=True):
    if symmetric:
        d = sp.diags(np.power(np.array(adj.sum(1)), -0.5).flatten(), 0)
        a_norm = adj.dot(d).transpose().dot(d).tocsr()
    else:
        d = sp.diags(np.power(np.array(adj.sum(1)), -1).flatten(), 0)
        a_norm = d.dot(adj).tocsr()
    return a_norm

def preprocess_adj(adj, symmetric=True):
    adj = adj + sp.eye(adj.shape[0])
    adj = normalize_adj(adj, symmetric)
    return adj

となっています。A_$\leftarrow \hat{D}^{-\frac{1}{2}}\hat{A}\hat{D}^{-\frac{1}{2}}$という処理ですね。ただし後の計算のために初めに単位行列を加えています。

ここからはレイヤーの中身を見ていきます。レイヤーはkegra/layers/graph.pyで定義されています。ここではfeed forwardの計算を定義しているcallの部分を取り出してみます。

from keras.engine import Layer
import keras.backend as K

class GraphConvolution(Layer):
    """Basic graph convolution layer as in https://arxiv.org/abs/1609.02907"""
    def call(self, inputs, mask=None):
        features = inputs[0]
        basis = inputs[1:]

        supports = list()
        for i in range(self.support):
            supports.append(K.dot(basis[i], features))
        supports = K.concatenate(supports, axis=1)
        output = K.dot(supports, self.kernel)

        if self.bias:
            output += self.bias
        return self.activation(output)

featuresが前の層の出力$H^{(l)}$で、basisがグラフ構造G=$\hat{D}^{-\frac{1}{2}}\hat{A}\hat{D}^{-\frac{1}{2}}$です。for文がありますが、デフォルトではself.support=1なので、1つのグラフ構造に対してのみ畳み込みを実行します。outputは $$ \hat{D}^{-\frac{1}{2}}\hat{A}\hat{D}^{-\frac{1}{2}}H^{(l)}W^{(l)}+\text{bias} $$ となります。最後に活性化関数に通してGraph Convolution Layerの出力となります。

次はtrain.pyに戻ってmodelの定義を見てみます。

modelの定義

train.pyにあるmodelは次のようになっています。

__________________________________________________________________________________________________
Layer (type)                    Output Shape         Param #     Connected to                     
==================================================================================================
input_2 (InputLayer)            (None, 1433)         0                                            
__________________________________________________________________________________________________
dropout_1 (Dropout)             (None, 1433)         0           input_2[0][0]                    
__________________________________________________________________________________________________
input_1 (InputLayer)            (None, None)         0                                            
__________________________________________________________________________________________________
graph_convolution_1 (GraphConvo (None, 16)           22944       dropout_1[0][0]                  
                                                                 input_1[0][0]                    
__________________________________________________________________________________________________
dropout_2 (Dropout)             (None, 16)           0           graph_convolution_1[0][0]        
__________________________________________________________________________________________________
graph_convolution_2 (GraphConvo (None, 7)            119         dropout_2[0][0]                  
                                                                 input_1[0][0]                    
==================================================================================================
Total params: 23,063
Trainable params: 23,063
Non-trainable params: 0

図で表すと次のようになります。

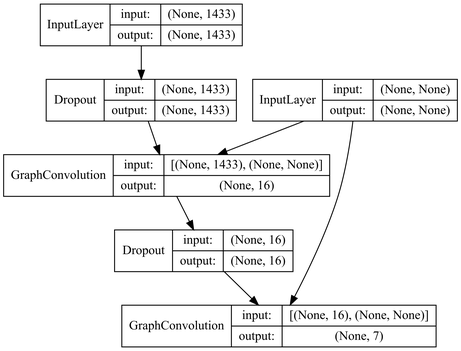
重みを畳み込む際にグラフ構造を引数としています。1433の単語を畳み込みで処理して、各ノードに要素数7のベクトル（ソフトマックス）を出力している感じです。

コードは以下のようになっています。

X_in = Input(shape=(X.shape[1],))

# Define model architecture
# NOTE: We pass arguments for graph convolutional layers as a list of tensors.
# This is somewhat hacky, more elegant options would require rewriting the Layer base class.
H = Dropout(0.5)(X_in)
H = GraphConvolution(16, support, activation='relu', kernel_regularizer=l2(5e-4))([H]+G)
H = Dropout(0.5)(H)
Y = GraphConvolution(y.shape[1], support, activation='softmax')([H]+G)

# Compile model
model = Model(inputs=[X_in]+G, outputs=Y)
model.compile(loss='categorical_crossentropy', optimizer=Adam(lr=0.01))

model.fit(graph, y_train, sample_weight=train_mask,
              batch_size=A.shape[0], epochs=1, shuffle=False, verbose=0)

入力は