(著)山たー
Graphical Lassoを用いることで変数間の関係をグラフ化できます。遺伝子データについて遺伝子のネットワーク解析などに使います。今回は、遺伝子データが無かったので、Boston Housing Dataの各変数間の関係をグラフ化してみます。
コード
ライブラリのインポート
グラフの描画のためにpydotとGraphvizが必要です。
import pydot import numpy as np import pandas as pd import seaborn as sns from matplotlib import pyplot as plt from sklearn.datasets import load_boston from sklearn.covariance import GraphLasso import scipy as sp
GraphLasso
#X:データ, alpha:L1正則化パラメータ, disp_heatmap:結果を表示するかどうか
def Graphical_Lasso(X, alpha, disp_heatmap=True):
#データの正規化(必須)
X=sp.stats.zscore(X,axis=0)
#GraphLasso
model = GraphLasso(alpha=alpha,verbose=True)
model.fit(X)
cov=np.cov(X.T) #計算による分散共分散行列(転置を取るかはデータの向きによる)
cov_ = model.covariance_ #スパース化した分散共分散行列
pre_ = model.precision_ #スパース化した分散共分散行列の逆行列
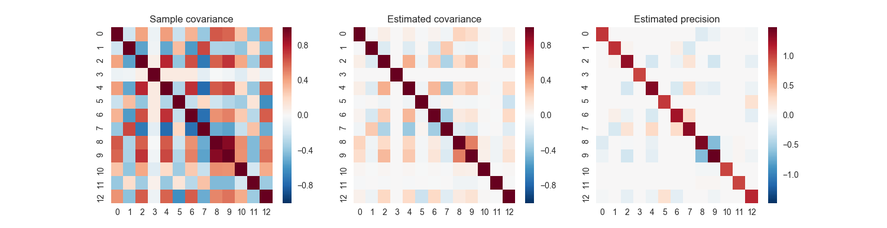
#分散共分散行列のヒートマップによる表示
if disp_heatmap==True:
f, axes = plt.subplots(1, 3, figsize=(15, 4))
axes[0].set_title('Sample covariance')
axes[1].set_title('Estimated covariance')
axes[2].set_title('Estimated precision')
sns.heatmap(cov, ax=axes[0])
sns.heatmap(cov_, ax=axes[1])
sns.heatmap(pre_, ax=axes[2])
return model
グラフの表示
グラフの表示についてはPythonでGraphvizを使ってマルコフチェーンを描画するを参考にしました。各ノードの色は結合しているエッジの数に応じて濃くなるようにしました。
def Disp_Gaussian_Graphical_Model(model,feature_names):
pre_ = model.precision_ #スパース化した分散共分散行列の逆行列
#グラフ表示のために対角成分は0にする
pre_zero=pre_-np.diag(np.diag(pre_))
#分散共分散行列の逆行列(≒隣接行列)からグラフを生成する
g = pydot.Dot(graph_type='graph')
df = pd.DataFrame(index=feature_names.tolist(),
columns=feature_names.tolist(),
data=pre_zero.tolist())
#ノードを追加
for c in df.columns:
node = pydot.Node(c)
g.add_node(node)
#エッジを追加
for i in df.index:
for c in df.columns:
if c>=i:
#エッジの絶対値が0.1より大きいときに表示(ここは好みによる)
if abs(df.loc[i, c]) > 0.1:
edge = pydot.Edge(g.get_node(i)[0], g.get_node(c)[0],
penwidth=5*abs(df.loc[i, c]))
edge.set_label('{:.1f}'.format(df.loc[i, c]))
g.add_edge(edge)
#結合数によって色を変える
nodeList = g.get_node_list()
num_edges=np.sum(abs(pre_zero) > 0.1, axis=0)
max_num_edges=max(np.amax(num_edges),1)
for i in range(len(df.index)):
node = nodeList[i]
# H S Vの順 Sを変更
color=str(0)+" "+str(num_edges[i]/max_num_edges)+" "+str(1)
node.set_color("black") #nodeの輪郭の色
node.set_fillcolor(color) #nodeの中身の色
node.set_style('filled')
# グラフを出力
#g.write_png('LassoEstimatedGGM.png', prog='neato')
g.write_png('LassoEstimatedGGM.png')
拡張BICの計算
def Compute_extended_BIC(model,n,p,cov,gamma):
omega = model.precision_
E=(np.sum(np.sum(omega != 0, axis=0))-p)*0.5
#尤度
MLE=n*(np.log(np.linalg.det(omega))-np.trace(np.dot(cov,omega)))
EBIC=-MLE+E*np.log(n)+4*E*gamma*np.log(p)
return EBIC
https://skggm.github.io/skggm/tour
Extended Bayesian Information Criteria for Gaussian Graphical Models
を参考にしました。
main関数
def main():
#Boston Housing Dataをインポート
boston = load_boston()
X=boston.data
feature_names=boston.feature_names
cov=np.cov(X.T) #標本分散共分散行列
#普通はn(サンプル数)>p(変数の数)なので
n=max(X.shape[0],X.shape[1]) #サンプル数
p=min(X.shape[0],X.shape[1]) #変数の数(ノード数)
#Graphical Lassoの実行
alpha=0.4 #L1正則化パラメータ
model=Graphical_Lasso(X, alpha)
#BIC, EBICの計算
BIC=Compute_extended_BIC(model,n,p,cov,0)
print("BIC :"+str(BIC)+" alpha :"+str(alpha))
EBIC=Compute_extended_BIC(model,n,p,cov,0.5)
print("EBIC :"+str(EBIC)+" alpha :"+str(alpha))
#グラフ化
Disp_Gaussian_Graphical_Model(model,feature_names)
if __name__ == '__main__':
main()
結果
λ=0.4のとき
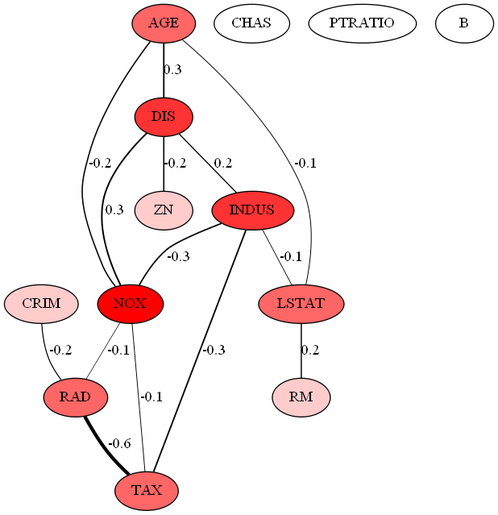
λ=0.2のとき
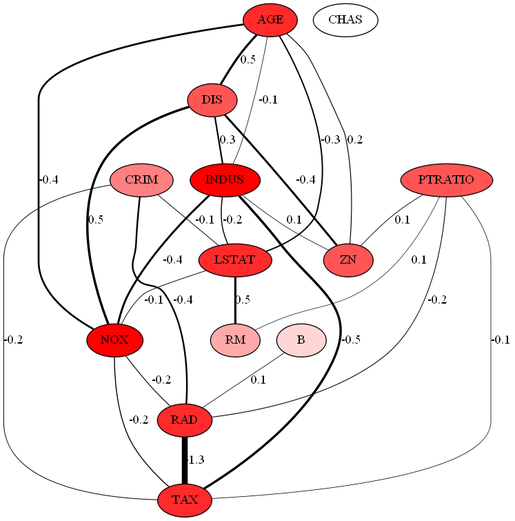
※RADとTAXの間は1.3ではなく、"-"がエッジに隠れているので、-1.3です。
各ラベルの意味は次の通りです。
CRIM=人口 1 人当たりの犯罪発生数
ZN=25,000 平方フィート以上の住居区画の占める割合
INDUS=小売業以外の商業が占める面積の割合
CHAS=チャールズ川によるダミー変数 (1: 川の周辺, 0: それ以外)
NOX=窒素酸化物(NOx)の濃度
RM=住居の平均部屋数
AGE=1940 年より前に建てられた物件の割合
DIS=5 つのボストン市の雇用施設からの距離 (重み付け済)
RAD=環状高速道路へのアクセスしやすさ
TAX=$10,000 ドルあたりの不動産税率の総計
PTRATIO=町毎の児童と教師の比率
B=町毎の黒人 (Bk) の比率
LSTAT=給与の低い職業に従事する人口の割合 (%)
scikit-learn に付属しているデータセットから引用しました。
グラフの見方はいろいろですが、ハブを見るというのが1つの方法としてあるそうです。
拡張BICによるモデルの選択
拡張BIC(Extended Bayesian Information Criteria;EBIC)を最小にするL1正則化パラメータを選ぶことで、モデルの選択を行うことができます。p>>nのときはγの値を0より大きくします。γ=0のときはBICと同じです。
最適なモデルを選ぶ関数
def Compute_BEST_GGM_from_extended_BIC(X,n,p,cov,gamma):
alphas = np.linspace(0, 1, 100)
#alphas=np.array([0.1,0.2,0.3,0.4])
num_alphas=alphas.shape[0]
EBICs=np.zeros(num_alphas) #EBICを記録する配列
for i in range(num_alphas):
alpha=alphas[i]
model=Graphical_Lasso(X, alpha,False)
#BIC, EBICの計算
EBIC=Compute_extended_BIC(model,n,p,cov,gamma)
print("EBIC :"+str(EBIC)+" alpha :"+str(alpha))
EBICs[i]=EBIC
#正則化パラメータに対するEBICの値のグラフ
plt.plot(alphas, EBICs)
plt.xlabel("L1 regularization parameter (alpha)")
plt.ylabel("extended BIC (EBIC)")
plt.show()
#最適なmodelのインデックスを取得
best_idx=np.argmin(EBICs)
best_alpha=alphas[best_idx]
best_model=Graphical_Lasso(X, best_alpha)
return best_model,best_alpha
main関数(変更版)
def main_select_best_model():
#Boston Housing Dataをインポート
boston = load_boston()
X=boston.data
feature_names=boston.feature_names
cov=np.cov(X.T) #標本分散共分散行列
#普通はn(サンプル数)>p(変数の数)なので
n=max(X.shape[0],X.shape[1]) #サンプル数
p=min(X.shape[0],X.shape[1]) #変数の数(ノード数)
model,alpha=Compute_BEST_GGM_from_extended_BIC(X,n,p,cov,0.5)
print("Best alpha :"+str(alpha))
#グラフ化
Disp_Gaussian_Graphical_Model(model,feature_names)
if __name__ == '__main__':
#main()
main_select_best_model()
結果
正則化パラメータを0~1まで変更してEBICを計算しました。最適となったのは正則化パラメータが0.86のときでした。
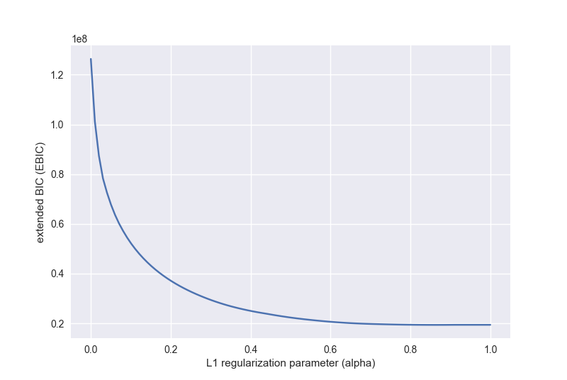
このときの推定された分散共分散行列とその逆行列は以下のようになりました。

グラフは以下のようになりました。

RADとTAXのみ、負の相関関係があるという結果になりました。RADが高速道路へのアクセスのしやすさで、TAXが不動産税率ですから、高速道路にアクセスしやすいほど税率が高くなるという直接的な関係があると意味づけられます。ただ、extended BICの実装を間違えている可能性もあるので、正しい結果とは断定できません。
コメントをお書きください
優曇華院 (Saturday, 31 March 2018 03:00)
こいつ…医学部じゃねえ…!
makoto (Sunday, 26 August 2018 16:33)
拝見させていただきました。
こちらですが、中ほどのコードで0.1以上でつながりがあるようにされていますが(好みによると記載されている部分)、このようにデータの中に、直接的なsourceやtargetが指定されているタイプではなく、データ間の類似性からネットワークを構築する手法についてより詳細に理解できる参考資料等はほかにございますでしょうか?
山たー (Sunday, 16 September 2018 01:57)
makotoさん
コメントに気づきませんでした。すみません。
自分はネットワーク解析についてあまり詳しくないので、適当に記事を書いてしまった覚えがあります。
一応、この記事は
川野 秀一, 松井 秀俊, 廣瀬 慧, スパース推定法による統計モデリング (統計学One Point), 共立出版, 2018
を参考にして書きました。それゆえ、スパースモデリングを取り扱った本を参考にすると良いと思います。
licht (Monday, 07 February 2022 11:40)
code上、精度行列の要素=偏相関係数と見做している?点、ご確認いただけないでしょうか。
精度行列(pre_)から偏相関係数を算出する時は
corr(i, j) = pre_(i, j) / sqrt( pre_(i,i) * pre_(j. j))
の式で算出が必要という理解です。
https://www.quora.com/How-can-I-get-the-partial-correlation-matrix-using-the-covariance-matrix-for-my-data-taking-the-inverse-doesnt-work-as-mentioned-in-other-threads-below